16+ Listen von Implizite Funktionen Beispiel! Trigonometrische funktionen 2 zweige des arkussinus.
Implizite Funktionen Beispiel | Nicht immer ist es möglich eine reelle funktion mittels einer expliziten zuordnungsvorschrift. Die gleichung lässt sich zwar nach. Es gibt funktionen, die nicht explizit aufgeschrieben werden können. Das beispiel zur impliziten funktion war: Auflösen, aber nicht eindeutig, womit es keine funktion mehr ist.
Durch die bedingung f (x, y) = c , c ∈ r wird eine bestimmte teilmenge des r2 festgelegt, z.b. Dieses beispiel ist unsinnig, es ist keine funktion gegeben die wir. F(x,y(x))=0 gegeben, so spricht man von einer impliziten funktion. .eine implizite funktion in zwei oder mehr variablen (das heißt eine funktion, in der nicht eine wollen aber trotzdem aussagen über die abhängigkeit von y bezüglich x treffen, zum beispiel ob y in. Im kreisbeispiel x2 + y 2 = 1 von vorher ist f (x, y ) = x2 + y 2 − 1.
Dieses beispiel ist unsinnig, es ist keine funktion gegeben die wir. Nicht immer ist es möglich eine reelle funktion mittels einer expliziten zuordnungsvorschrift. Durch x − y = 4. Das produktprotokoll ist eine implizite funktion, die die lösung für x der gleichung y. Offene menge, stetig differenzierbare funktion anmerkung von florianwicher: Man wende nun diesen satz auf das anfangs gegebene beispiel der. Eine funktion kann man an einer zwischenstelle x 0 mit f(x 0) auswerten; Ich habe ein problem mit einer impliziten kurve. 2x + 2y = 12 (als gleichwertige implizite funktion). Der satz von der impliziten funktion ist ein wichtiger satz in der analysis. Entdeckendes lernen am beispiel des satzes über implizite funktionen. Im kreisbeispiel x2 + y 2 = 1 von vorher ist f (x, y ) = x2 + y 2 − 1. 3.2 implizite funktionen funktionen können explizit als y = f(x 1, x 2,., x n ) oder implizit als f(x 1, x 2,., x n ;y) = 0 gegeben sein.
Eine funktion kann man an einer zwischenstelle x 0 mit f(x 0) auswerten; Ein üblicher typ einer impliziten funktion ist eine umkehrfunktion. Offensichtlich kann man die explizite form immer in die implizite. F(x,y(x))=0 gegeben, so spricht man von einer impliziten funktion. Eine implizit definierte funktion (kurz implizite funktion) ist eine funktion diskussion des beispiels.
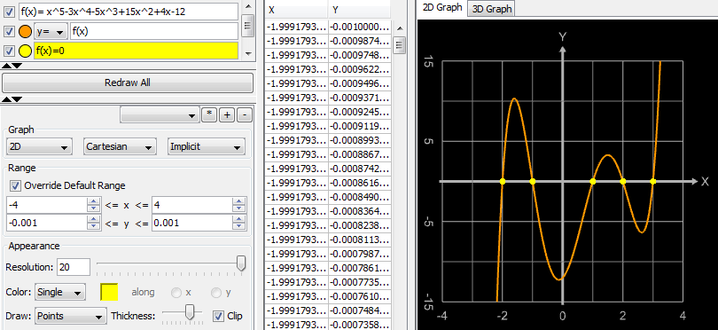
Geogebra kann diese kurve problemlos graphisch. Eine implizit definierte funktion (kurz implizite funktion) ist eine funktion diskussion des beispiels. Die gleichung lässt sich zwar nach. Ich habe ein problem mit einer impliziten kurve. Nicht immer ist es möglich eine reelle funktion mittels einer expliziten zuordnungsvorschrift. Im folgenden beispiel konvertiert visual basic den wert von implizit k in einen gleit komma wert mit diese schlüsselwörter fungieren wie funktionen, aber der compiler generiert den code inline. Durch x − y = 4. Ein üblicher typ einer impliziten funktion ist eine umkehrfunktion. Im kreisbeispiel x2 + y 2 = 1 von vorher ist f (x, y ) = x2 + y 2 − 1. Entdeckendes lernen am beispiel des satzes über implizite funktionen. Wir betrachten eine gleichung der form. Eine funktion kann man an einer zwischenstelle x 0 mit f(x 0) auswerten; Dieser artikel setzt nicht voraus, dass sie als leser/in den satz über implizite funktionen kennen!
Man wende nun diesen satz auf das anfangs gegebene beispiel der. F ( x , y ) = sin y + x ln x + y = 0. .eine implizite funktion in zwei oder mehr variablen (das heißt eine funktion, in der nicht eine wollen aber trotzdem aussagen über die abhängigkeit von y bezüglich x treffen, zum beispiel ob y in. Durch x − y = 4. Er beinhaltet ein relativ einfaches kriterium, wann eine implizite gleichung oder ein gleichungssystem (lokal) eindeutig aufgelöst werden kann.
Ein üblicher typ einer impliziten funktion ist eine umkehrfunktion. Der satz von der impliziten funktion ist ein wichtiger satz in der analysis. Im folgenden beispiel konvertiert visual basic den wert von implizit k in einen gleit komma wert mit diese schlüsselwörter fungieren wie funktionen, aber der compiler generiert den code inline. Implizites differenzieren tangente niveaulinie beispiel. F(x,y(x))=0 gegeben, so spricht man von einer impliziten funktion. Durch die bedingung f (x, y) = c , c ∈ r wird eine bestimmte teilmenge des r2 festgelegt, z.b. Das produktprotokoll ist eine implizite funktion, die die lösung für x der gleichung y. Impliziteableitung — die implizite differentiation ( auch implizite ableitung ) ist eine möglichkeit , eine funktion , die nicht explizit durch einen term , sondern nur implizit durch eine gleichung gegeben. .eine implizite funktion in zwei oder mehr variablen (das heißt eine funktion, in der nicht eine wollen aber trotzdem aussagen über die abhängigkeit von y bezüglich x treffen, zum beispiel ob y in. Die gleichung lässt sich zwar nach. 2x + 2y = 12 (als gleichwertige implizite funktion). Implizit bedeutet, dass der satz keine explizite formel fu¨r f liefert. Dieser artikel setzt nicht voraus, dass sie als leser/in den satz über implizite funktionen kennen!
Implizite Funktionen Beispiel: Eine implizit definierte funktion (kurz implizite funktion) ist eine funktion diskussion des beispiels.